技術読本「機構解析の解法」

「機構解析」の一般的な定式は、運動方程式にジョイントなどの拘束条件を伴う微分代数方程式で、この式を解くことで構成部品（ボディ）の挙動を求めています。微分代数方程式は、DAE（Differential Algebraic Equation）とも記述されます。

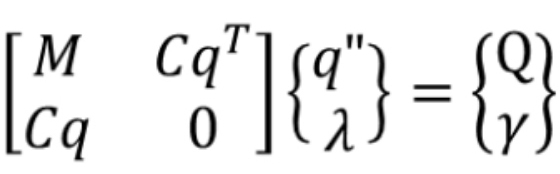
M ：ボディの質量マトリックス
Cq ：ジョイント拘束から導かれるマトリックス
q”：ボディの６方向加速度（q：変位）
𝜆：ジョイントに発生する力とトルク
Q：ボディに作用する力のベクトル
γ ：ジョイント拘束から導かれるベクトル

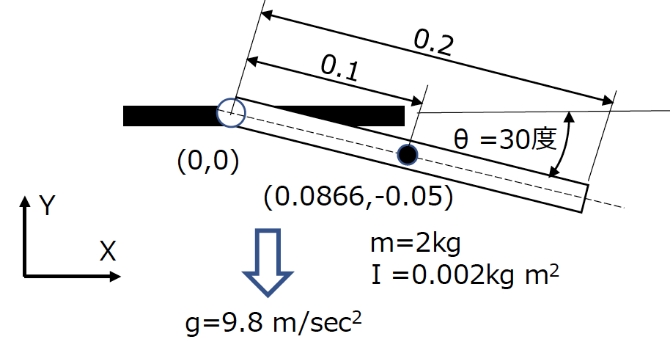
機構解析の解法例を、回転ジョイントで拘束された２次元の単一振り子問題で説明します。

回転ジョイント拘束では、拘束位置(0, 0) は変化しませんので、振り子重心位置(x(t), y(t))は次の式になります。

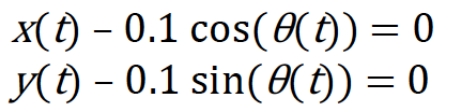
この式より変位拘束式𝐶を設定でき、この拘束式よりヤコビアンと呼ばれる𝐶𝑞 を求めます。ヤコビアンは、拘束式をボディの変位x, y, θ で偏微分した式になります。

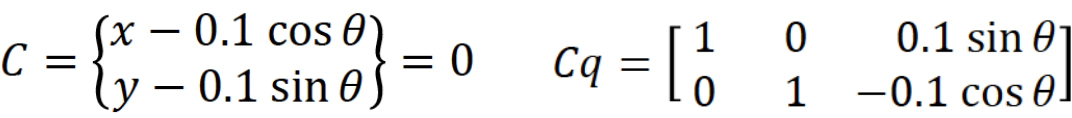
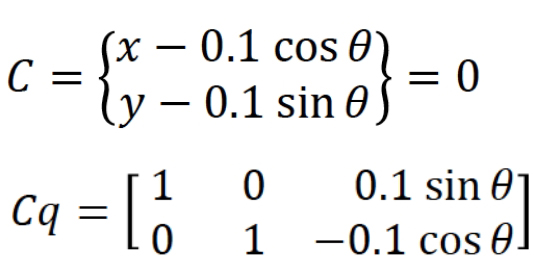
微分代数方程式の中の𝛾は、変位拘束式から導かれる加速度拘束式から得られるマトリックスで、回転ジョイントの場合は次式になります。

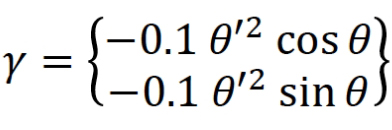
質量マトリックス𝑀と重力による外力𝑄を次式で与えることで、単一振り子の微分代数方程式を設定できます。

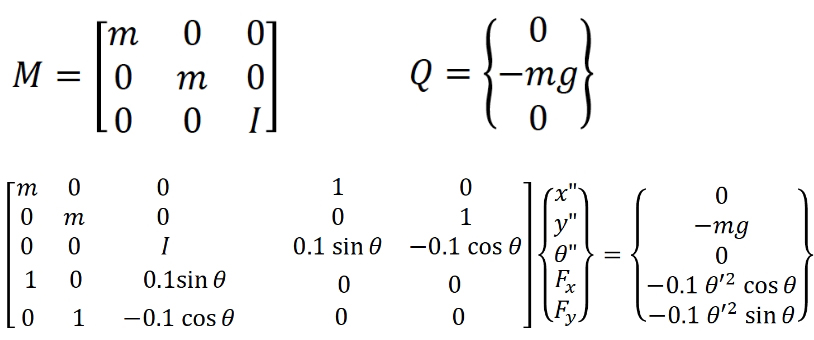
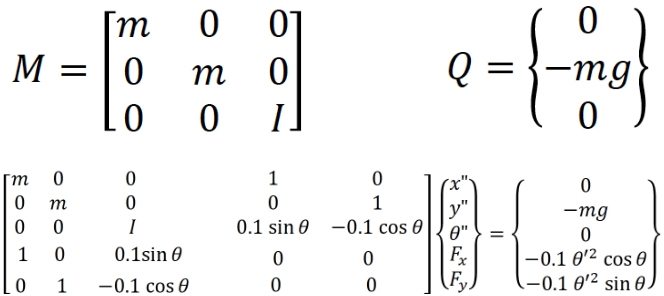
この式で、m=2kg, I=0.002 kg m^2, -mg=-2*9.8N は一定の値です。
時刻t = 0 sec では、𝜃=−𝜋/6rad 、𝜃′=0rad/sec ですので、微分代数方程式は次式となり、この式を解くことで、加速度𝑥𝑥”y”𝜃𝜃”を計算できます。

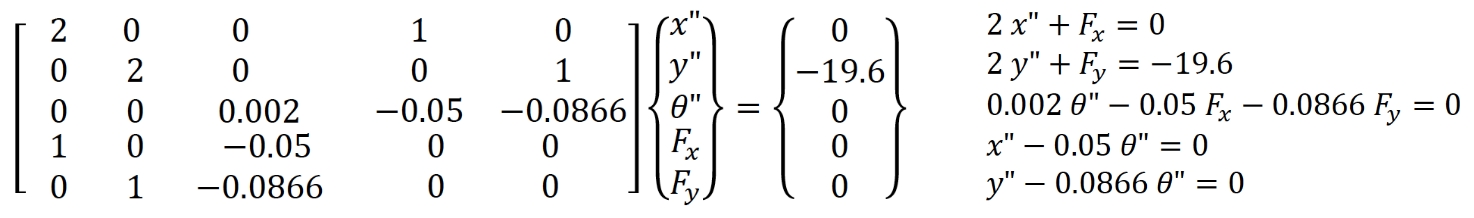
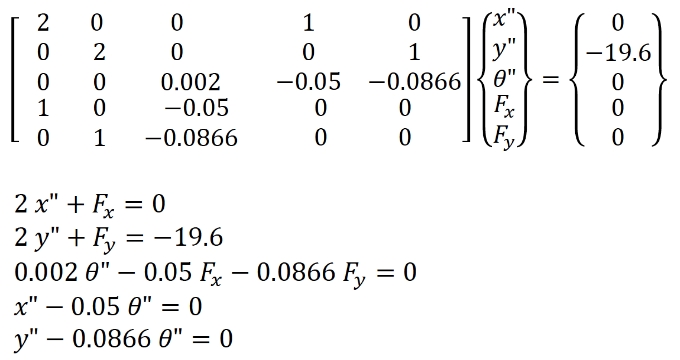
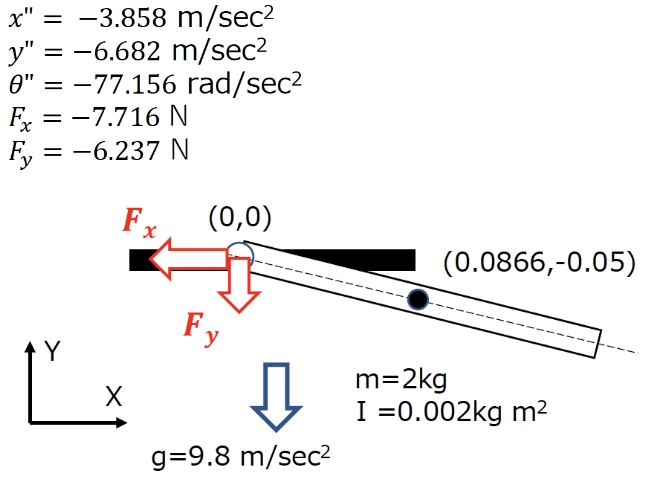
この式の解は以下になります。加速度を解析時間刻みΔtで積分して速度、さらに積分して変位を求めます。その値を、微分代数方程式に代入して、次の時間ステップの動きを計算します。

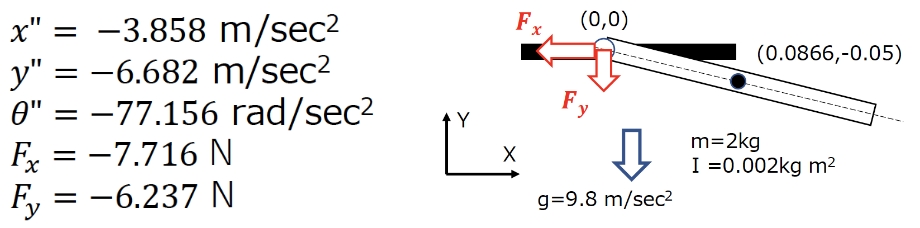
積分には、基本的な常微分方程式の数値解法であるオイラー法がありますが、ルンゲ・クッタ法がより実用的な解法とされています。