最適化
Optimization
RecurDyn環境に統合された設計最適化機能であるRecurDyn/AutoDesignを使用することにより、多くの機械システムの設計で必要とされる設計変数の最適化を、容易な操作で行うことが可能です。
AutoDesignの特徴
- RecurDynとシームレスな直感的インターフェースにより、設計変数と目的関数を容易に定義、およびカスタマイズが可能です。
- 世界初のプログレッシブメタモデルアルゴリズム、および以下の最適化技術により、非常に少ない試行回数での最適化が可能です。
・設計変数のスケールが異なる問題を解決するマルチスケール最適化技術
・目的数に関係なく使用できる、簡単で強力な多目的最適化アルゴリズム - 設計変数として、パラメーター値や弾性体形状を使用できます。
- 目的関数や制約条件には、数式/弾性体応力結果/結果スコープ/ProcessNetを使用できます。

AutoDesignの機能
設計スタディ
DOE(実験計画法)を実施し、効果分析や設計変数のスクリーニングを行う機能です。以下の6つの手法が使用可能です。
- 拡張プラケットバーマン
- 完全実施要因計画
- 3水準直交配列
- レベルバランス記述的計画
- Bose直交配列
- 2水準直交配列
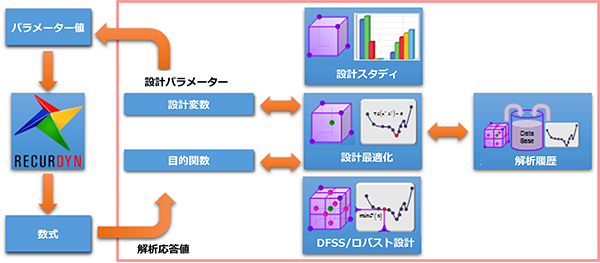
最適化機能
設計最適化
メタモデルによる逐次近似最適化(SAO)を用いて、少ない試行回数でパラメーター最適化を行います。メタモデル手法として、以下の3つが使用可能です。
- 同時クリギング法 (Simultaneous Kriging Method)
- 放射基底関数法 (Radial Basis Function Method)
- 保守的応答曲面法 (Conservative Response Surface Method)
DFSS/ロバスト設計
逐次近似最適化を使用し、公差などを考慮した実行可能な最適解を探索します。
得られた最適解を複数のサンプリング点を使用して検証することも可能です。
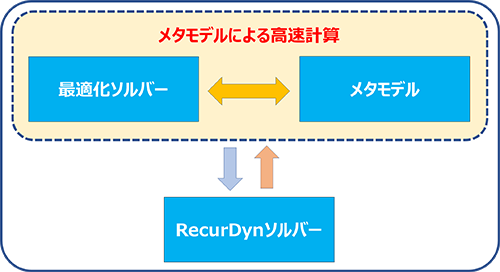
*逐次近似最適化:
初期DOEによるサンプル点の結果からメタモデルを作成し、最適化プロセスで計算された新たな結果でメタモデルを逐次更新することで精度を良化させ、少ない計算数で最適化する手法
信頼性解析
信頼性解析では2つのアルゴリズムを使用し、システムの故障確率を求めることができます。
SAO法では従来よりも少ないサンプリング数で合理的な結果を得ることができます。
- SAOハイブリッド法:
メタモデルを使用し、故障確率や信頼性指標を計算します。
試行回数は非常に少ないです。 - モンテカルロ法:
精度の良い結果を得るには多くの試行回数を必要としますが、大域的な評価が可能です。
Case study
二輪小型モビリティ
安定姿勢制御のための最適なフィードバックゲインの同定
- 要件
-
- モビリティは静止状態から 2m/s まで加速
- 目標速度と実際の速度差を最小化
- ドライバーは安全な姿勢を維持
設計変数:フィードバック制御におけるP,I,Dゲイン
目的関数:ターゲットとの速度差

- 最適化された設計値
-
- Pゲイン 10000 → 500
- Iゲイン 10 → 870
- Dゲイン 10 → 608
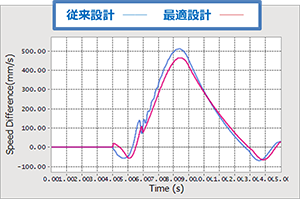
速度差のグラフ
解析計算回数 34回

